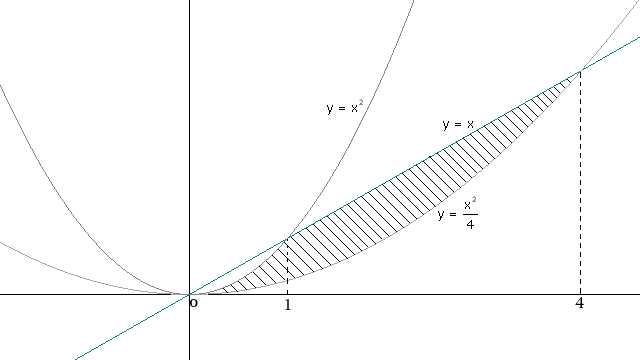
Calcúlese el área del recinto limitado por las curvas y=x, y=x², y=x²/4

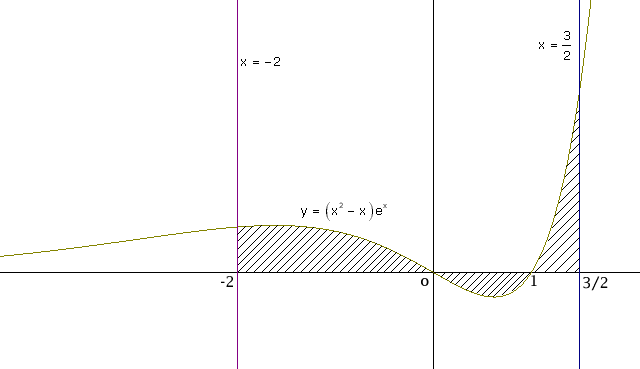
Hállese el área de la región limitada por la curva y=(x²-x)e^x, el eje OX y las rectas x=-2 , x=3/2.

Calcular el área de la región limitada por las curvas y²=2px , x²=2py.

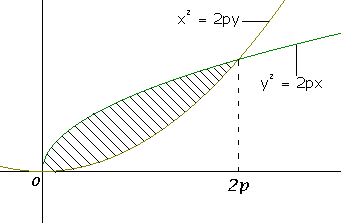
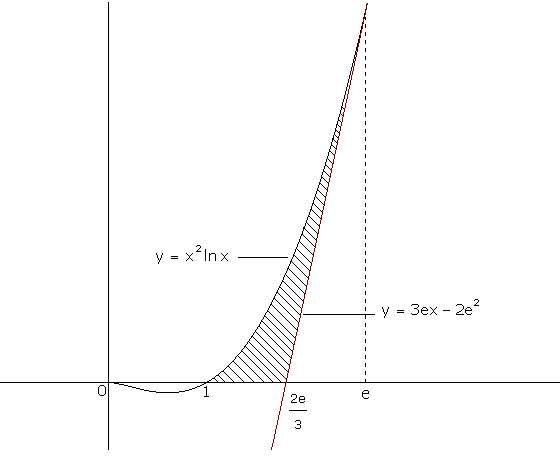
Determinar el área comprendida entre la curva y=x²lnx , la recta tangente a dicha curva en x=e y el eje OX.

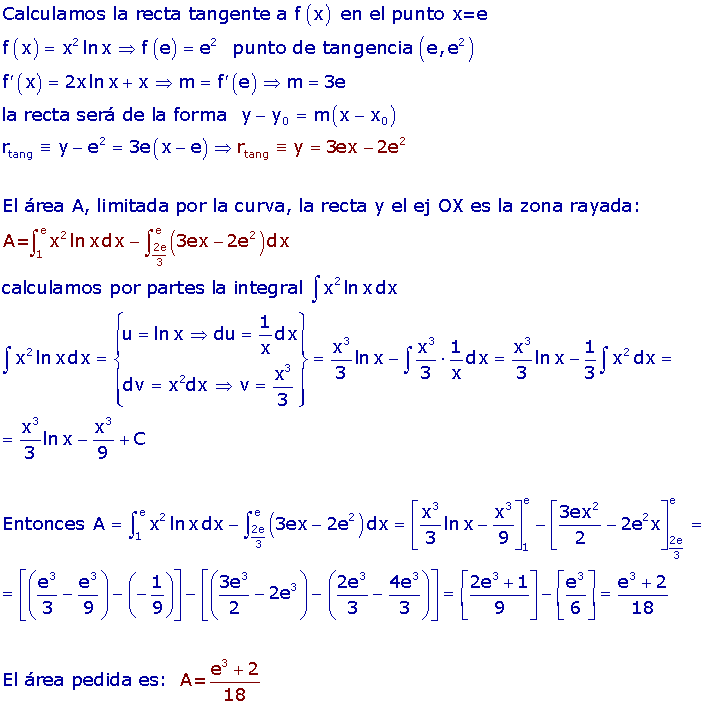
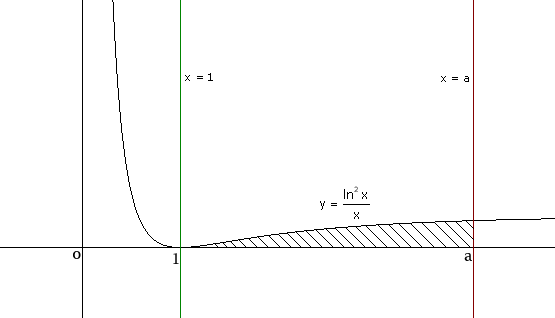
Encontrar un número a>1 para que el área limitada por la curva y=(ln²x)/x , el eje de abscisas y las rectas x=1 y x=a sea 9.

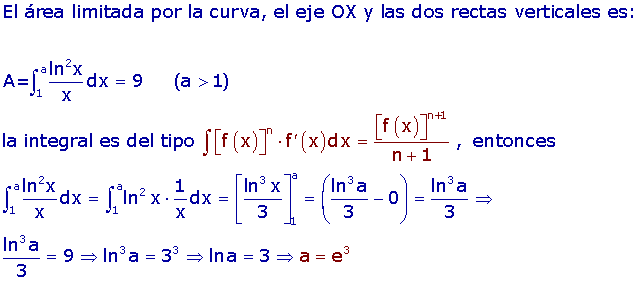
Hállese el área de la región comprendida entre la curva y=1/(1+x²)  y la parábola 2y=x².

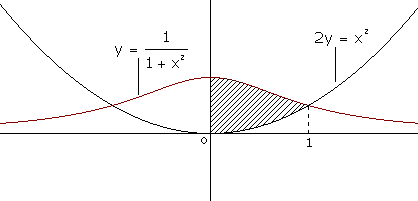
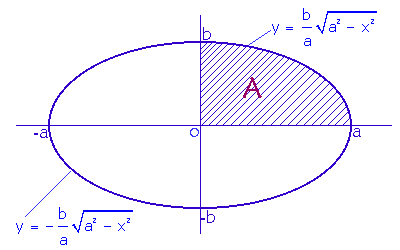
Calcular el área de la región encerrada por la elipse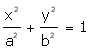 

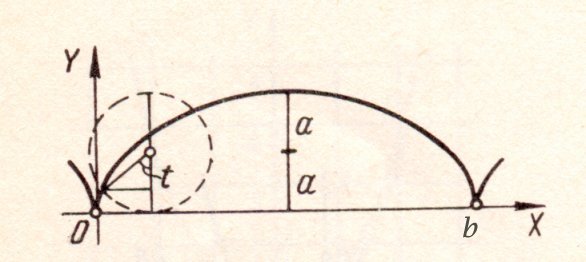
Hallar el área de la región limitada por el eje OX y el arco completo de la cicloide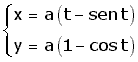 

Sea la función real de variable real definida por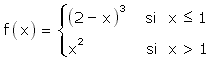 

1. Razonar si la función es continua en toda la recta real.
2. Razonar si la función es derivable en toda la recta real.
3. Determinar el área encerrada por la gráfica de la función y por las rectas y=8 , x=0 , x=2.